Reasoning, the pinnacle of human cognition, occurs both by logic and by association. Logic and word-based thinking have been extensively studied; however, the role of association, although recognized, retains mysterious elements.
Here’s a typical stance. Colin Martindale remarks (p 148),We have seen that the creative act involves the discovery of an analogy between two or more ideas or images previously thought to be unrelated. The discovery does not result from logical reasoning but, rather, emerges as a sudden insight.
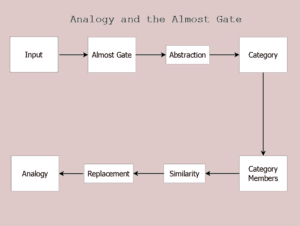
The phrase “sudden insight” has no explanatory value. In Mental Construction the features of induction, intuition, and creative acts are given shape–they are based on neural networks which self-organize data into data clusters (patterns) which reoccur many times. The iterated sequence of Almost Gate and Hebb’s Law leads to analogies and associative category identity. We experience this variously as creativity, insight, discovery, and various words which capture a novel relationship supported by the similarities.
Let’s be more explicit about human reasoning. Although we are most conscious of thinking in words, there is a before-conscious cognitive aspect, prior to the verbal arena, in the brainstem and limbic system. Association reigns supreme there, prior to the assignment of names by the dominant hemisphere. Names denote patterns of set characteristics. The interaction of names and patterns across the corpus callosum will follow.
This has been touched on in the earlier discussion, especially of neural threshold and neural cascade.
Definition of Reasoning
Consider two definitions in Merriam-Webster Dictionary:
Reasoning – the drawing of inferences or conclusions through the use of reason
Inferences – a conclusion or opinion that is formed because of known facts or evidence
Combining them, we arrive at a constructive definition. Reasoning is the process of drawing inferences in order to form a conclusion or judgment.
Why Do We Reason?
We reason to increase the likelihood of our continued life. That is not directly the same as the evolutionist claim that all actions are encouraged or discouraged according to the effect on passing on one’s genes.
People are not always rational. That is usually taken to mean irrational or wrong; however, many times our thoughts follow an associative path, a path of similarities. Our thoughts proceed not only by logic, but by similarity. In this sense our thought may be described as non-logical, but that doesn’t mean the thought is unreasonable. As discussed in Building the Brain, the 3S’s (Satiety, Sex, Safety) shape our behavioral choices before logical rationality even makes its appearance in the human brain. When we see a long, dark shape in the grass. Is it unreasonable to react as if it is a snake, even though all the information necessary is not yet available? No, the similarity to a snake makes precautions reasonable.
Figure 19.1 shows the two reasoning modes with three contrasted features. Association uses patterns and similarities to rapidly draw inferences. Logic uses words and rules to draw conclusions.
Inference Methods
An inference is a derivation of conclusions from given information or premises by any acceptable form of reasoning. Inferences are commonly discussed as occurring by two methods, which align with association and logic.
- Induction uses association. Induction uses association of patterns to draw a general conclusion from concrete cases.
- Deduction uses logic. Deduction extracts conclusions by applying rules to its premises.
Before a closer look in deduction and induction, a quick mention of two specialized inferential methods is in order. These methods were discovered by laborious efforts over centuries. They require training and careful attention to apply correctly. Their worth is high, but they are not in use by the typical person is everyday thinking. Their use requires considerable effort of mental energy.
- Probability, which relies on frequencies within a known domain to reach conclusions on the stated likelihood.
- Statistical reasoning, which indicates that, on average, a certain percentage of a set of entities will satisfy the stated conditions. This style of reasoning is necessitated when entities of non-binary truth value are considered. For instance, the occurrence of cancer in a country’s population. Cancer has many forms, so detailed information about cancer details is ignored in the statistical count. Similarly, the population, as individuals, have different propensities towards cancers. Since neither the item of interest or the range of its action have a binary truth value, statistical reasoning not deductive reasoning is called for.
Hypothetical-deductive reasoning, the useful combination of association and logic of the scientific method, is discussed in Mental Construction Model.
Induction
What is meant by induction? The Encyclopedia Britannica defines induction’s two aspects in this manner.
1. Induction. The inference of a generalized conclusion from particular instances
2. Inductive reasoning means reasoning from known particular instances to other instances and to generalizations. There are several major kinds of inductive reasoning, including causal inference, categorical inference, and analogical inference.
The snake reaction above is based on induction thinking. The person sees a dark, thin shape in the grass. Before he determines more, he startles away from the object, fearing that it’s a snake that could bite him. He generalized from the dark, thin shape to a snake based on partial knowledge. And he acted on it before further examination revealed if it were a snake or perhaps a fallen branch. This reaction cost little and lowered a potential danger.
Unfortunately, it is possible to draw false conclusions. The black swan case is notorious. For centuries Europeans had only observed white swans. They concluded all swans were white. However, Western Australia provided examples of black swans, disproving the conclusion. Such a conclusion, from incomplete information which is the predominant state of our knowledge, inductive.
Deduction
Deduction uses logical rules upon facts of undoubted certainty and relationships of unbreakable validity. If its requirements are met, then its conclusion is valid. Deduction is often referred to as reasoning from the general rule to the specific case. The specific case is an example of a deductive inference. The validity of a deductive argument assumes unassailable premises (or facts) for an unquestionable conclusion.
Exemplar.
- A union B => C. When A is True and B is True, then C will be true.
- This conclusion is undeniable. The argument is logically valid.
- The problem comes when we apply the logical conclusion to the real world. Facts have uncertainty.
- A union B => C. Also our belief in A is most likely true (75%). Our belief in B is also most like true (75%).
- There is uncertainty in the truth of the conclusion. It is less than undeniable.
- There are various formulas to calculate the uncertainty (like, the minimum of the premises)
In addition to our knowledge being incomplete, the words we use in our statements truncate reality this way and that way, such that pure A and B premises make multiple assumptions which are hidden. A quick example is “We went to war in Iraq.” It wasn’t a declared war. And which time, 1990 or 2003?
When you look at your conscious decision-making process, you will surely find more than two premises, A and B, upon which your decision rests.
The point is not that deduction is bad or to be avoided, but that generalization from limited data is essential and supports our application of deduction to real life situations.
Non-Rationality
Rational action is action that satisfies one’s desires. Reason mediates between desires (goals) and beliefs (knowledge). Competing desires and beliefs arise from emotional valences of the 3S’s, not from logical, cost-benefit analyses.
Rationality implies being based on or in accordance with reason or logic. Rationality is closely linked to logic in speech. Logical has come to be applied to only deductive logic, excluding inductive reasoning. Therefore many people equate rationality with logic, but that is highly restrictive. If an association leads to a useful analogy that leads to action that satisfies one’s desires, then we have satisfied the rational requirement (satisfying one’s desires) without using deduction.
There is a verbal choice in how one describes that successful inductive performance.
- We have achieved rationality without deductive logic
- Or, irrationality does not deserve the opprobrium of madness or insanity as it does in many common conversations.
Why Ever Induction?
Since induction can allow you to make errors and deduction never does, why ever use induction?
An important reason is that deductive logic, although exact, is sterile. It’s bound to its premises. It can never grow beyond its premises.
The Internet Encyclopedia of Philosophy, in its article “Deductive and Inductive Arguments” makes the point this way.Because deductive arguments are those in which the truth of the conclusion is thought to be completely guaranteed and not just made probable by the truth of the premises, if the argument is a sound one, then we say the conclusion is “contained within” the premises; that is, the conclusion does not go beyond what the premises implicitly require.
Think of sound deductive arguments as squeezing the conclusion out of the premises within which it is hidden.
For this reason, deductive arguments usually turn crucially upon definitions and rules of mathematics and formal logic.
Limitation of Reasoning
Imperfect theoretical understanding despite complete facts limits one’s ability to complete to definitive conclusions. A good example comes again from the stock market. Despite complete trade information, the lack of a general theory of stock prices means that many buy/sell regimes exist, with none definitive.
Associations supporting matches which are not perfect can easily lead to false conclusions. Like a scientist, one must reject an association that leads to a contrary fact.
Analogies, a significant type of inductive thinking depends on the Almost Gate and Hebb’s Law.
A new question arises from the Mental Construction viewpoint. How can logic be accomplished in a neural brain when everything is abstraction and association?