Merriam Webster defines deduction this way.
The deriving of a conclusion by reasoning; specifically inference in which the conclusion about particulars follows necessarily from general or universal premises.
The Internet Encyclopedia of Philosophy describes the restriction of deduction in its discussion of “Deductive and Inductive Arguments.”
[I]f the premises are true, then it would be impossible for the conclusion to be false.… Think of sound deductive arguments as squeezing the conclusion out of the premises within which it is hidden.
The syllogism is a very basic logical deduction
- All men are mortal
- Socrates is a man
- Therefore, Socrates is mortal
It’s so simple that it’s easy to glide over its significance. The Internet Encyclopedia of Philosophy gives a valid deductive argument which is a step up in complexity, yet it remains easy to understand.
It’s sunny in Singapore. If it’s sunny in Singapore, then he won’t be carrying an umbrella. So, he won’t be carrying an umbrella.
Logic in Use
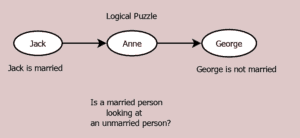
For a more complicated use of logic, consider the logical puzzle in Figure 21.1, which is difficult but has a similarity to real-life situations where some information isn’t available.
- Jack is looking at Anne, but Anne is looking at George
- Jack is married
- George is not married
Is a married person looking at a non-married person?
Keith Stanovich (p 70–72) uses this puzzle to illustrate a distinction between people who readily perform logical analysis and those who take eschew that effort. Here, for Mental Construction, the example shows the power of logical deduction whether a person chooses the effort to employ it or not.
Many people say there’s not enough information to solve the puzzle, but only two cases need to be considered. Case 1, Anne is married. Case 2, Anne is unmarried.
In case 1, Anne, who is married, is looking at George who is not married. So the puzzle answer is Yes. In case 2, Jack, who is married, is looking at Anne who is not married. So the puzzle answer is Yes. Both cases yield an affirmative answer to the puzzle question. Thus, the puzzle answer is Yes.
Granted, we don’t always examine logical problems that closely, but the puzzle reveals that difficult questions can sometimes be resolved with close deductive analysis. Just how does our pattern-matching, category-abstracting neural brain accomplish logical operations?
No Logic until learned
The ability to reach logical conclusions on the basis of prior information is central to human cognition. Yet, it is generally agreed that the state of our knowledge regarding the mechanisms underlying logical reasoning remains incomplete and highly fragmented.
– “The Reasoning Brain: The Interplay between Cognitive Neuroscience and Theories of Reasoning” in Frontiers in Human Neuroscience
Where do we get the idea that objects can be linked together, that if either this or that is present, then a consequence will follow? How do we come up with premises to derive logical conclusions from? Deductive logic is exact. Yet to deduce truth, the premises must be 100% true. Premises include relationships between facts as well as the facts themselves. Those premises are culled and restricted to items of interest based on our internal needs, emotions, and personal sensory data. However they can also include facts, interpretations, and predictions that other people we respect or follow make.
There’s no special neuron areas hard-wired for syllogisms. How do we accomplish logical thinking?
Logic from Experience
- We learn simplified logic by repeated occurrences of patterns, without the need for instruction.
- More consequentially, we learn the logic built into language, through feedback from others.
Logic arises as assemblages of neurons that act in a coordinated fashion upon being struck by inputs that have seen repeatedly This action on abstracted input is like that of self-organized map (SOM). The linkage of various inputs must be consistently related.
Initially, we identify objects in our environment. We categorize. We truncate. We generalize. Some of these basic patterns precede our learning language; however, once we have language, its words and phrases inevitably shape the patterns we use linguistic relativism, the weak Sapir-Whorfian theory.Learning Logic in a Neural Network
A deductive argument depends on the facts in its premises being true and the use of logical relationships. An experimental example of a necessary step to learn logic, categorizing logical terms.
Obviously, we can’t examine a child’s neuron when he’s learning logic and language. However, we can test the idea in a controlled experiment with an artificial neural network which has already shown its ability to develop a Self-Organized-Map (SOM). Most of the logically thinking an individual does is based on if things happen together, if something isn’t happening when another something is, and if something follows (or doesn’t) other things happening. That is, AND, OR, NOT, and IF-THEN.
An artificial neural network does not possess the subtle gradations of action potentials of human brain neurons nor the immense number of interconnections they support, but it has the advantage of simplicity that can reveal gross regularities of action that are swamped by the magnitude of actual neural networks. Of course, Einstein’s dictum – Make things as simple as possible, but not simpler – is a sobering constraint.
This is a demonstration of the learning of a very simple, but essential property that a neural brain needs to process information logically. This neural network learns to associate proposition with logical terms. The logical terms are AND, OR, NOT, XOR, and IT-THEN.
Kohonen Network Features
The Kohonen neural network has 2 layers. The input layer has 5 neurons, while the receiving layer, has 100 neurons. Of that 100 neurons, the winning neuron alone will fire its axon, sending a signal to all the neural layers which lie downstream of it.
The initial state of the neural is that all neurons have a random efficiency in all its connections. This random efficiency is akin to the amount of transmission of electric potential divided by the total electric potential received at a random synapse. The randomness substitutes for neurons which have not developed any preference for coordinated firing. The neurons have not learned any relationships between various input signals, yet.
The Kohonen artificial neural network is interconnected in a specific pattern. Each input neuron is connected to each neuron in the receiving layer. Also, each neuron in the receiving layer is connected with every other neuron in the receiving layer. These receiving layer interconnections have a particular feature—the neuron that wins (receives the highest total electrical potential from the inputs) feeds the closest neurons an excitatory potential while those farthest away receive an inhibitory potential.
The particular wiring of the Kohonen neural network has been shown to settle, after repeated occurrences of inputs, to a winning neuron for distinct inputs. This may sound very arbitrary but cortical layers have been found to
- have a very consistent patterns of inputs and outputs
- use both excitatory and inhibitory neurotransmitters.
Input Data
The input data is specified in this form.
- First row describes the Kohonen network shape plus the number of data rows
- Input layer: 5 neurons in 1 column
- Receiving layer: 10 neurons in 10 columns
- Data rows: 18 rows of data
- Second row is first row of data to be processed, in the Kohonen neural network
- 1st T indicates first proposition in logical expression has a positive truth value
- 2nd T indicates second proposition in logical expression has a positive truth value
- 3rd through 5th T are considered together as the code for AND
- All data rows have the same form, T or F for the 2 propositions used in the logical expression and a set of 3 T or F to indicate the logical expression (AND, OR, NOT, IF-THEN, and XOR)
- The fourteenth data row
- First, T is an indication that the first proposition has a truth value of true
- Second, F is an indication that the second proposition has a truth value of false
- Third, Fourth, and Fifth, TTF, is the code for IF-THEN
- Two special notes about the data rows
- IF-THEN only has two rows. If T, then T and If T then F, because they are the only cases that match to sensible cases. In formal logic, the two cases in which the antecedent is F are also defined. These lead to nonsensical conclusions, such as … No one uses such these implications in normal thoughts. Equivalences allowed in formal logical based on false antecedents (such as …) can surface in computerized logic systems. That is worrisome.
- The NOT logical operator only requires 1 input proposition. The Kohonen neural network, as set it up, requires 2 input propositions. To allow for this, the NOT operator has 4 rows in which the 2nd proposition takes both truth values irrespective of the 1st proposition’s truth value. See data rows 9 to 12.
Receiving Layer
After 5202 exposures to input rows, the receiving layer settled on 18 different winning neurons. From then on, the Kohonen network distinguished between each case. Downstream from the receiving layer, the propositional truth value and the logical expression will be considered as a group, for further refinement.
Kohonen Learning Insights
The logical operator code was learned through repeated exposure by the network. Thereafter the logical code along with the inputs are linked together. They will be grouped in any processing downstream of this information.
- The number of cycles is large; however, this is unsupervised learning. A supervised child, upon learning words and receiving feedback, will typically abandon its idiosyncratic, internal code for logical operations, and use common words like and, or, not, and so on, learning more quickly.
Logical thoughts are at the summit of our thinking, but there is no special mental circuitry in our genetics to perform deductive logic. Instead we have dedicated neural areas most likely clustered in the prefrontal lobes, to extract logical patterns from groupings of information, learned through repeated experience with the aid of language.
Logic in Language
One way to look at language is that language gives to its speaker wisdom discovered by ancestors. Language gives us solutions (categories, words) that organize reality in a manner that has proven useful. Each of us individually would never have come up with so many and so useful categories on our own. As Ralph Waldo Emerson put it, Language is fossil pottery.
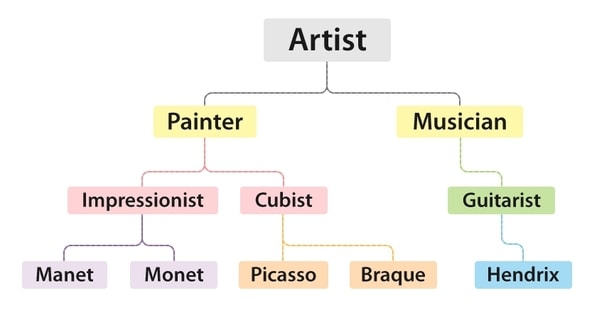
Consider Figure 21.3, a hierarchy of words describing artists. One’s knowledge of the hierarchy is formed over time. Also, the level of distinction between artists can vary by the level of abstraction. People may mean both Pablo Picasso and Jimi Hendrix when they say artist. Yet if painters are speaking, Hendrix may be excluded from their consideration. The hierarchy of artists is not a natural categorization (which Plato saw as carving nature at its joints), but a conventional one. Language often provides hierarchies which are conventional, that have proven their worth through utility.
In addition to the categorization and hierarchies, language provides logical concepts to link together our observations. This person AND that person were present. IF either that action OR that other action was taken, THEN a good result followed. No, she was NOT at the meeting. That ALWAYS happens. SOMETIMES he follows rules. Simple, fundamental logical operations can be constructed in language. People differ in how careful they are in their statements, but the potential utility is there. In classes and person reading, the skill of logic can be developed much further, yet it possible to still run into problems using logic.
Expanding Knowledge
If one wishes to expand knowledge it can’t be done deductively, because it is constrained by its premises. Something more is needed – creativity, inspiration, and leap of faith are various names for it. Next, Mental Construction deals with creativity, the positive side of associative thinking.